The FAST tracking algorithm

In order to optimally track objects over time, FAST uses machine learning to optimally integrate information across multiple features. This page details the theory behind this tracking algorithm.

Please note that this page is heavily based on chapter 3 of the thesis 'Collective twitching motility in Pseudomonas aeruginosa and its evolutionary consequences'.

Throughout this page, the term `feature' will be used in a generic sense. It can in principle be applied to any quantitative property of an object, however in FAST's default state the set of features is restricted to object centroid ($x$,$y$), length, width, area, orientation, and the mean and standard deviation of the pixel intensities associated with the object in each imaging channel. These are the features available for measurement using the feature extraction module. Following measurement, these features are stored as a feature vector $\mathbf{f}_{t,i}$ for object $i$ in frame $t$. In subsequent sections, the subscript $i$ will generally be omitted for brevity. Depending on context, $\mathbf{f}_{t}$ will also sometimes be expressed as $f_{t,\phi}$, allowing explicit indexing over each feature $\phi$.

Fig. 1: Illustration of concepts used in FAST's tracking algorithm. a) Illustrative theoretical tracking dataset. Particles (green) move between two separate frames in dataset (arrows) from initial positions (white circles) to final positions (grey circles). Tracking is hampered by detection errors, movement of objects into and out of the imaging frame, and apparent merging of touching objects. b) Feature space representation ($\mathbf{f}$) of data shown in (a). Centroid coordinates $x$ and $y$ are used in this example for ease of understanding, but in general $x$ and $y$ can be supplemented or replaced by any feature. For example, a third feature dimension, object brightness ($m$), is not shown here. c) Displacement space representation ($\Delta \mathbf{f}$) of $x$ and $y$. `True negatives' are incorrect links that are rejected by the discrimination threshold $\beta_t$, `true positives' are correct links that are accepted, `false negatives' are correct links that are rejected and `false positives' are incorrect links that are accepted. The `optimal threshold' indicates a theoretical window in this space that would optimally discriminate between correct and incorrect links.

As a concrete example of the problems posed by single-object tracking in high-density, high-velocity datasets, figure 1a represents a theoretical dataset consisting of a set of point-like particles flowing from the top to the bottom of a square imaging frame. It will prove useful throughout this page to consider moving objects from two perspectives: the first is the feature space representation $\mathbf{f}$ (figure 1b), which represents the absolute instantaneous positions of objects in the global feature space. The second is the displacement space representation $\Delta \mathbf{f}$ (figure 1c), which simply represents the movement of objects within $\mathbf{f}$ between two frames relative to their positions in the first frame. For illustrative purposes, figure 1 is restricted to just two features, the object centroid coordinates ($x$ and $y$). However, in general both $\mathbf{f}$ and $\Delta \mathbf{f}$ are composed of as many dimensions as there are features.

The main challenge for tracking-by-detection frameworks such as that used by FAST is suppression of incorrect links generated by detection errors, object overlap and movement of objects into/out of the frame. These result in spurious potential links (`negatives') being generated by distance-based metrics. To minimise spurious links, the obvious approach is to apply a distance threshold in $\Delta \mathbf{f}$ such that links that fall outside of its range are suppressed. Unfortunately, we can see that this dataset poses several challenges that render this simplistic approach non-optimal. Firstly, there is a motion bias towards the bottom of the frame. Using the simple distance threshold would therefore either unfairly filter out large movements downwards or incorrectly assign links implying the upward movement of objects. This is the problem of feature drift. Additionally, movements are more tightly clustered along the $x$-direction than the $y$-direction. Even if drift is accounted for, any isotropic window will either be too lenient in accepting large changes in $x$, or too harsh in rejecting large changes in $y$. This is the problem of feature anisotropy. The optimal acceptance window therefore needs to be shifted (to account for drift) and reshaped into an ellipse (to account for anisotropy).

A further problem comes from attempting to use additional features to improve the tracking algorithm. In the example shown, each object is also associated with a brightness $m$, perhaps indicating the quantity of a fluorescent protein within the object. If $m$ was both constant and perfectly measured, it would be possible to reconstruct tracks based purely on object brightness alone. Analogously, we might imagine placing a set of balls of unique shape and colour into an opaque box and shaking it - even though we would not be able to monitor the positions of the balls over time, we would still be able to determine which ball at box opening corresponded to which ball at box closing based on its unique appearance. In reality however, the brightness of these particles is subject to both measurement noise and variability. How can this brightness information be optimally integrated with the positional information?

This may appear to be a distinct problem, but we can actually understand it in terms of feature drift and anisotropy. To see this, imagine the axis $\Delta x$ in figure 1b was replaced with the change in particle brightness between frames, $\Delta m$. Let us suppose that measurement of $m$ causes photobleaching. We would then expect to see that this new data cloud was biased towards negative $\Delta m$ - in other words, that the feature $m$ had drifted between frames. In addition, noise will generate uncertainty in $\Delta m$, resulting in a spread about its `true' value. The problem therefore becomes how to combine this uncertainty in $\Delta m$ with that in $\Delta x$ and $\Delta y$, which is exactly the same as our problem of trying to compare the relative uncertainties of $\Delta x$ and $\Delta y$.

Another problem is that $\Delta \mathbf{f}$ is dynamic. For example, all the particles in the field of view may begin drifting upwards instead of down, average particle speed may increase, or the density of the system may change. Any adjustments made to compensate for the problems of drift and anisotropy must therefore be able to respond to these dynamic changes in the statistical properties of the system.

To formalise this discussion, let us assume that $\Delta \mathbf{f}_t$ is drawn from a multivariate normal distribution $\mathcal{N}(\mathbf{\mu}_t, \mathbf{\Sigma}_t)$ with mean vector $\mathbf{\mu}_t$ and covariance matrix $\mathbf{\Sigma}_t$. In general, the distribution for $\Delta f$ for any given feature $f$ need not be normal. However, the normal distribution is usually a good approximation, and the tools for manipulating the multivariate normal distribution are well developed. The evolution of objects in $\mathbf{f}$ can then simply be represented as:

\begin{equation} \mathbf{f}_{t+1} = \mathbf{f}_{t} + \mathbf{w}_{t}, \end{equation}

where $\mathbf{w}_t$ indicates a random vector drawn from the distribution $\mathcal{N}(\mathbf{\mu}_t, \mathbf{\Sigma}_t)$. The frame index $t$ is used here to emphasise that both $\mathbf{\mu}_t$ and $\mathbf{\Sigma}_t$ can vary dynamically through time.

This formulation is a very general way of expressing object motion through $\mathbf{f}$. Not only can it used to describe first-order features such as object position and orientation, it can also be used to describe higher-order features such as object velocity, acceleration and angular velocity. This allows motion correspondence-based approaches to be applied within the same framework. In the following sections, I will develop techniques to solve the previously described problems associated with high-density object tracking using this framework.

Fig. 2: Flowchart of major elements of the feature tracking algorithm. Different versions of the feature space (raw, $\mathbf{f}$, regularised, $\bar{\mathbf{f}}$ and normalised, $\hat{\mathbf{f}}$) are indicated at the points in the algorithm at which they are generated.

FAST adopts a two pronged approach to tracking (figure 2). The first prong is to make all features directly comparable by shifting and rescaling $\mathbf{f}$ to generate the normalised feature space $\hat{\mathbf{f}}_t$. The corresponding normalised displacement space $\Delta \hat{\mathbf{f}}_t$ is isotropic and zero-centred, resolving the problems of feature drift and anisotropy. $\Delta \hat{\mathbf{f}}_t$ is normalised on a frame-by-frame basis, allowing dynamic changes in the statistical properties of features to be captured and accounted for.

The second prong is to adaptively vary the detection threshold to account for variations in system density and feature usefulness. To assist in this second task, the concept of feature reliability is introduced. This is a joint measure of the noise associated with each feature and the range of values it can take, and represents the usefulness of each feature for distinguishing different link options in the normalised displacement space. Reliability can be combined across features to give a single trackability score for each timepoint. This is a user-directed heuristic measure of dataset quality which can be used for quality control and automated purging of low-quality sections of tracking datasets.

At the core of the FAST tracking algorithm is a machine learning protocol that automatically determines the necessary dataset statistics. A training set of object links is first created using a high stringency, classical tracking algorithm. This training set is then used to estimate the reliability of each feature and the trackability of the dataset, as well as the values of $\mathbf{\mu}_t$ and $\mathbf{\Sigma}_t$. These statistics are then used to generate $\Delta \hat{\mathbf{f}}_t$ and to calculate the adaptive threshold for each timepoint.

For simplicity, I will here limit the description of the tracking algorithm to the case that $\mathbf{\Sigma}_t$ is diagonal, i.e. that all features are independent from each other. Extension of the algorithm to the case where correlations exist between features is fairly simple, and is provided in the final section of this page. This is the version of the algorithm employed by the full version of FAST. However, as we will see, the assumption of feature independence makes the role of each mathematical operation easier to understand.

In the first stage of the tracking algorithm, the most easy to track objects in a given dataset are linked, and the resultant dataset mined for feature statistics. To provide some degree of balance between different features during training dataset creation feature scaling is first applied. Defining the maximum value of each feature in each frame to be $\max(f_{t,\phi})$ and the minimum value to be $\min(f_{t,\phi})$, the range of all features is set to between 0 and 1 using the equation:

\begin{equation} \bar{f}_{t,\phi} = \frac{f_{t,\phi} - \min(f_{t,\phi})}{\max(f_{t,\phi}) - \min(f_{t,\phi})}. \end{equation}

$\bar{f}_{t,\phi}$ will be referred to as the regularised feature space. A list of putative links between objects in frame $t$ and $t+1$ is then created, pairing cells according to the minimal Euclidean distance in the regularised feature space between them. To be explicit, the matrix $Q_{i,j}$ of Euclidean distances between objects $i$ in frame $t$ and $j$ in frame $t + 1$ is calculated as:

\begin{equation} Q_{i,j} = \|\bar{\mathbf{f}}_{t+1,j} - \bar{\mathbf{f}}_{t,i}\|, \end{equation}

where $\|\cdot\|$ indicates the Euclidean norm of the contents. Next, the unique score $q_{i}$ is found that satisfies the equation:

\begin{equation} q_{i} = \min_{j \in C_{t+1}}(Q_{i,j}), \end{equation}

where $C_{t+1}$ is the set of objects present in frame $t+1$. The links with scores $q_i$ are then sorted by score, and the proportion, $P$, of lowest scoring links classified as correct. $P$ is the first user-adjustable parameter of the algorithm.

One problem with this approach is that feature scaling tends weight low-quality and high-quality features equally. This can severely limit the accuracy of links based on the simple similarity metric $q_i$. To avoid this problem, the training dataset creation algorithm can be restricted to the $x$ and $y$ coordinates of the object centroid. These are generally quite robust features with similar amounts of noise, and can be used for the initial approximation of tracks. The user is therefore provided with the option of using all features during the low-fidelity linking stage, or just the centroid.

Next, these preliminary links $i$-$j$ are used to estimate $\Delta \mathbf{f}_{t,i}$ simply as $\Delta \mathbf{f}_{t,i} = \mathbf{f}_{t+1,j} - \mathbf{f}_{t,i}$. From this displacement space, $\mathbf{\mu}_t$ can be calculated as the sample mean of each feature:

\begin{equation} \mathbf{\mu}_t = \frac{1}{n_t}\sum^{n_t}_{i = 1} \Delta \mathbf{f}_{t,i}, \end{equation}

where $n_t$ represents the total number of training links made from timepoint $t$.

Under the simplifying assumption that $\mathbf{\Sigma}_t$ is diagonal, each element of the diagonal will represent the variance of the corresponding element of $\Delta \mathbf{f}_t$. To simplify notation, these variances will be written as the vector $\mathbf{\sigma}^2_t$. These are then given as:

\begin{equation} \mathbf{\sigma}^2_t = \frac{1}{(n_t-1)}\sum^{n_t}_{i = 1} (\Delta \mathbf{f}_{t,i} - \mathbf{\mu}_t)^2. \end{equation}

The normalised feature space can now be calculated as:

\begin{equation} \hat{f}_{t,\phi} = \frac{f_{t,\phi}}{\sigma_{t,\phi}}, \end{equation}

\begin{equation} \hat{f}_{t+1,\phi} = \frac{f_{t+1,\phi} - \mu_{t,\phi}}{\sigma_{t,\phi}}. \end{equation}

Feature normalisation provides a means of fairly weighting all features automatically. In effect, instead of drawing the optimal threshold shown in figure 1c, we have instead shifted and rescaled the points such that the `true' displacements fit within the isotropic (circular) discrimination threshold. This is extremely valuable, as it means we only need to externally define a single parameter (the radius of this threshold) rather than a separate parameter for each feature. We can therefore avoid the very large numbers of parameters generally associated with multi-feature approaches. However, at the moment we have no means of deciding what value this distance threshold (denoted here as $\beta_t$) should take to optimally reject false links while accepting true links.

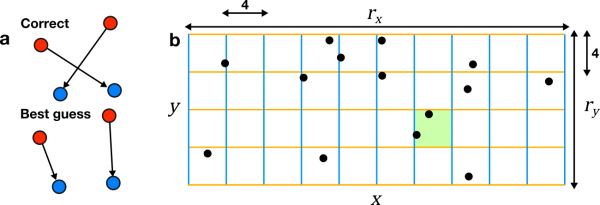Fig. 3: The problem of link ambiguity. a) Two objects in feature space at time $t$ (red) move to new positions at time $t+1$ (blue). The correct links differ from those assigned by the optimal guess based on available information. b) Partitioning of normalised feature space into regions of ambiguity by centroid features $x$ and $y$ from example shown figure 1. Each region of ambiguity is 4 standard deviations wide in each feature direction, corresponding to a 95% probability that an object at its centre will remain within its range in the next frame. The green region indicates a case where multiple objects are within a single region of ambiguity. The trackability of this dataset (number of regions = 40, number of objects = 13) is 0.49.

In FAST, $\beta_t$ is adaptively chosen to account for the problem of link ambiguity. As an informal introduction to this problem, consider the system in figure 3a. Two objects are moving through a normalised feature space between frame $t$ and $t+1$ - our task, as usual, is to assign links between the two frames. The best guess we can possibly make based on the information available to us is to link the nearest neighbours in this feature space. However, in reality, this assignment is incorrect. A good tracking algorithm should therefore be able to detect instances where such ambiguous assignments might occur, and suppress linking in these cases. (Note that these ambiguous links are distinct from the false links caused by mis-segmentations etc. as discussed in the overview section. These are in principle separate problems, but in practise a choice of $\beta_t$ stringent enough to suppress ambiguous links is also stringent enough to suppress false links.)

Why did the best guess fail? There are three contributory factors: movement unpredictablity, object proximity and insufficient feature information. If movement had been less noisy, the objects had been further apart, or more feature information had been available to distinguish the objects, the correct links would have been easier to make. To a certain extent, we have already accounted for movement unpredictability by normalising the feature space - the effect of noise will now at least be isotropic and zero-centred, allowing us to directly compare the contribution to ambiguity by each feature. But a measure still needs to be defined that allows us to estimate object proximity within this space. This is achieved within the FAST framework by defining object density within the normalised feature space.

To define a density, we require a measure of system volume. In this case, the domain of the normalised feature space (the range of object positions available within the space) will be approximated as a $\Phi$-dimensional hyperrectangle, where $\Phi$ is the total number of features in use. The (hyper-)volume of this object will then be used as the volume of the system. To measure this volume, the extent $e_{t,\phi}$ of each feature is first measured as double the inter-quartile range (IQR) of the feature across all objects at a given timepoint (in $\mathbf{f}_t$). The IQR is used in place of the full range as it is robust to statistical outliers and differing underlying feature distributions. Feature reliability $r_{t,\phi}$ is then simply defined as:

\begin{equation} r_{t,\phi} = \frac{e_{t,\phi}}{\sigma_{t,\phi}}. \end{equation}

Reliability is a scale-invariant and dimensionless statistic, allowing it to be directly compared between different features. Note that division by $\sigma_{t,\phi}$ occurs both when creating the normalised feature space and in the above equation - $r_{t,\phi}$ is therefore a metric of the size of the normalised feature space.

As a loose conceptualisation, reliability can be regarded as the number of regions of ambiguity each feature partitions the feature space into. If two or more objects are within the same region of ambiguity at time $t$, they cannot be reliably distinguished at time $t+1$. To be explicit, let us suppose that an object is at some position $\hat{f}_{t,\phi}$ in a one-dimensional normalised feature space. Under our assumption that $\Delta \hat{f}_{t,\phi}$ is a normalised Gaussian distribution, the object will move to a new position in the next frame within the range $\hat{f}_{t,\phi} - 2 < \hat{f}_{t+1,\phi} < \hat{f}_{t,\phi} + 2$ (one region of ambiguity) with probability 95%. If there is a single object within this range, the associated link is easy to assign. If there are multiple objects within this range at $t+1$ though, it will be difficult to distinguish the target object based upon this single feature alone. The object closest to the target object's starting position is most likely to be the target, but there is still a high probability that one of the other objects within this window is the true target.

As increasing numbers of features are added, the feature space is partitioned into more and more regions of ambiguity. To illustrate this effect, figure 3b shows the normalised $x$-$y$ feature space $\hat{\mathbf{f}}$ derived from the feature space shown in figure 1. The initially square domain has been stretched into a rectangle by the lower variability of movement in the $x$-direction than in the $y$-direction, corresponding to a greater value of $r_{t,\phi}$ for that feature. As a result, $\hat{\mathbf{f}}$ is split into 10 regions along the $x$-axis, while it is split into 4 along the $y$-axis. The total number of regions of ambiguity is therefore 40. This multiplicative property captures the effect of adding additional feature information - as more and more features are added, it becomes increasingly easy to unambiguously assign links across frames.

The density of the entire dataset, $d_t$, now captures the three factors contributing to link ambiguity into a single statistic by measuring the average number of objects per unit volume of the normalised feature space:

\begin{equation} d_t = n_t\prod^{\phi} \frac{1}{r_{t,\phi}}. \end{equation}

where $n_t$ is the number of objects detected at time $t$.

A more user-friendly statistic, the trackability, is calculated as $k_t = -\log_{10}(d_t)$. This statistic is useful for evaluating the ease of tracking for the entire dataset, considering the reliability of the information available from all features. Use of $k_t$ implicitly assumes that objects are uniformly distributed through feature space. This is unlikely to be true, especially in biological systems where cell division will lead to localised high-density patches. But it can still be a useful heuristic for deciding which timepoints to include in the full analysis. For example, hard-to-track frames (caused by, for example, temporary loss of focus in the original timecourse) appear as dips in the plot of $k_t$ against time.

Of course, this concept of `regions of ambiguity' is somewhat artificial. In reality, the ambiguity of assignment decreases smoothly as the separation of two objects in feature space increases. We can see in figure 3b several examples of objects sufficiently close to one another for links to be ambiguous, but which are assigned to separate regions of ambiguity. Instead, the critical measure is the number of unrelated objects that appear within the threshold defined by $\beta_t$ - these are the objects which might be falsely assigned to.

This number can be estimated from $d_t$: we begin by noting that $\beta_t$ is the radius of a $\Phi$-sphere in frame $t+1$ centred on the position of an object in frame $t$. This $\Phi$-sphere isolates a volume from the total volume of the system, and if this volume randomly contains an unrelated object, link assignment becomes ambiguous. Assuming objects are uniformly distributed throughout feature space, the $\Phi$-sphere is small relative to the entire feature space and $d_t$ is low enough that two unrelated objects are unlikely to be within the boundary of the $\Phi$-sphere, the probability $p$ of a random object appearing within the $\Phi$-sphere is approximately the density of the system multiplied by the volume of the $\Phi$-sphere:

\begin{equation} p \approx \frac{d_t \beta_t^\Phi \pi^\frac{\Phi}{2}}{\Gamma(1 + \frac{\Phi}{2})}, \end{equation}

where $\Gamma()$ indicates the gamma function. To assign $\beta_t$, the user defines a target ambiguous assignment probability $p$. This is then transformed to $\beta_t$ through the above equation for each timepoint. Note that $\beta_t$ is calculated according to the metric of the normalised feature space, meaning it is not reliant upon the ad-hoc definition of `regions of ambiguity' previously discussed.

Defining $\beta_t$ in this way allows us to automatically change the stringency of the tracking algorithm according to the properties of the dataset. When a system is at low density or the degree of movement is small, ambiguous links will occur fairly rarely and link assignment need not be very stringent. At the other extreme, with high levels of system noise or high system density, ambiguous links will be common. Links should therefore only be assigned when the evidence for object identity between frames is extremely strong, i.e. $\beta_t$ should be made extremely small to ensure that incorrect links are not accepted.

To perform high-fidelity tracking, we now determine link scores $\hat{Q}_{i,j}$ in a similar fashion as during the creation of the training dataset. However, the normalised feature space is instead used:

\begin{equation} \hat{Q}_{i,j} = \|\hat{\mathbf{f}}_{t+1,j} - \hat{\mathbf{f}}_{t,i}\|. \end{equation}

In assigning links from the matrix $\hat{Q}_{i,j}$, many tracking algorithms optimise the set of links given the scores of all putative links using matching methods such as the Hungarian algorithm or the Hopcraft-Karp algorithm. However, the extra information provided by additional features is usually sufficient to determine a single, unambiguous link between object $i$ and the set of objects at the next timepoint. As these more advanced matching algorithms are computationally expensive, FAST employs a simple greedy algorithm to assign links: given a matrix of putative link scores, the lowest score is taken and the corresponding link marked as correct. The sets of scores corresponding to the $i$ and the target object are then eliminated, and the next lowest scoring link marked as correct. This algorithm loops until scores raise above $\beta_t$; scores above this threshold are considered to correspond to false links, and linking for these objects is suppressed.

This initial linking run will miss objects that mis-segment in frame $t + 1$ but segment properly in frame $t + 2$ (or higher). To close these gaps, once all objects associated with links made between frames $t$ to $t + 1$ have been removed, $\hat{Q}_{i,j}$ is recalculated for objects $i$ in frame $t$ and objects $j$ in frame $t + 2$. Because the normalised displacement space is an isotropic multivariate Gaussian distribution, we can assume that the movement of an object through it is diffusive. Its displacement from its starting position should therefore be proportional to $\sqrt{\tau}$ (where $\tau$ is the lag between the starting time and the currently considered timepoint). To account for this, the threshold $\beta_t$ to is raised to $\sqrt{2} \beta_t$ for this second linking step. This assignment is repeated between frames $t$ and $t + \tau$ for all values of $\tau$ up to a user-defined maximal gap closure parameter. At each value of $\tau$, the value of $\beta_t$ is rescaled to $\sqrt{\tau}\beta_t$.

Multi-frame tracks are then extracted from the feature datasets based on the previously calculated frame-frame linkages. Tracks below a certain, user-defined length are removed. Typically, these short tracks correspond to temporary mis-segmentations, image artefacts or debris, and are not useful during further analysis stages.

The tracking algorithm described in the previous sections can easily be adapted to permit detection of cellular divisions. Divisions are events that are associated with large but predictable jumps in feature space from mother to daughter cells. For example, in the case of the division of P. aeruginosa, division typically causes area and length to halve, while the position of daughter cells can be inferred from mother cell length and orientation.

To initialise the division tracking algorithm following the feature tracking algorithm, separate versions of $\mathbf{f}$ are constructed from the feature vectors associated with the beginning and ends of those tracks constructed in the previous section. These vectors represent the states of daughter cells at birth and mother cells at division, respectively. $\bar{\mathbf{f}}$ and $\hat{\mathbf{f}}$ are now generated in a similar fashion as before, with two crucial differences: firstly, $\mathbf{\Sigma}$ and $\mathbf{\mu}$ are calculated from the set of feature vectors compiled across all timepoints. This compensates for the comparatively low number of divisions present in the dataset, and prevents statistical noise from dominating $\hat{\mathbf{f}}$. Secondly, a model is applied that predicts the feature vector of two daughter cells based on the feature vector of each mother cell. For example, the length of each daughter cell is predicted as half that of the mother, but the orientation of the daughters remains the same as for the mother. The training dataset $\bar{\mathbf{f}}$ is then generated based on links made between this predicted feature dataset (based on the maternal cell's $\mathbf{f}$) and the actual feature dataset (based on the daughter cell's $\mathbf{f}$). Feature normalisation and discrimination threshold selection is then applied by treating the predicted daughter feature vectors as $\mathbf{f}_t$ and the actual daughter feature vectors as $\mathbf{f}_{t+1}$. Links are assigned as described in the previous section.

From the equation at the end of the introductory section, we have:

\begin{equation} \mathbf{f}_{t+1} = \mathbf{f}_{t} + \mathbf{w}_{t}, \end{equation}

where $\mathbf{w}_t$ indicates a random vector drawn from the distribution $\mathcal{N}(\mathbf{\mu}_t, \mathbf{\Sigma}_t)$ with location $\mathbf{\mu}_t$ and covariance matrix $\mathbf{\Sigma}_t$.

$\mathbf{\mu}_t$ can be calculated from the training feature displacement set $\mathbf{f}_{t,i}$ simply by finding the sample average for each feature, as for the uncorrelated case. To relax the requirement that $\mathbf{\Sigma}_t$ be diagonal, it can be estimated as the sample covariance matrix:

\begin{equation} \boldsymbol{\Sigma}_t = \frac{1}{n_t-1} \sum_{i=1}^{n_t} (\Delta \mathbf{f}_{t,i} - \mathbf{\mu}_t) (\Delta \mathbf{f}_{t,i} - \mathbf{\mu}_t)^\intercal, \end{equation}

for each link in the training dataset, $i$ to $n_t$.

To generate the normalised feature space $\hat{\mathbf{f}}_t$, we need to find some transformation matrix $\mathbf{B}$ that can be applied to $\mathbf{f}_{t+1}$ and $(\mathbf{f}_{t+1} - \mathbf{\mu}_t)$ to set $\mathbf{\Sigma}_t$ to the identity matrix of equivalent dimension; this is also known as a whitening transformation. For a given covariance matrix $\mathbf{\Sigma}_t$ there are theoretically an infinite number of whitening transformations, but FAST applies the uniquely-defined transformation based on the eigendecomposition of $\mathbf{\Sigma}_t$:

\begin{equation} \mathbf{\Sigma} = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^{-1}. \end{equation}

Noting that $\mathbf{\Lambda} = \mathbf{\Lambda}^{\frac{1}{2}}\mathbf{I}\mathbf{\Lambda}^{\frac{1}{2}}$ and that $\mathbf{U}^{-1} = \mathbf{U}^\intercal$, the whitening transform $\mathbf{B}$ is then given as:

\begin{equation} \mathbf{B} = \mathbf{\Lambda}^{\frac{1}{2}}\mathbf{U}^\intercal. \end{equation}

The normalised feature space is then given as:

\begin{equation} \hat{\mathbf{f}}_{t} = \mathbf{B}_t\mathbf{f}_{t}, \end{equation}

\begin{equation} \hat{\mathbf{f}}_{t+1} = \mathbf{B}_t(\mathbf{f}_{t + 1} - \mathbf{\mu}_t). \end{equation}

Feature reliability is not easy to define in this new space, as $\mathbf{B}_t$ will not in general preserve the orientation of the feature axes. This contrasts to the case when $\mathbf{\Sigma}_t$ was diagonal, where $\mathbf{B}_t$ scaled the feature space parallel to each feature axis. However, the volume of the space can still be defined as the (hyper)volume of the $\Phi$-parallelotope corresponding to the transformed feature domain, i.e. the parallelotope with corners at positions $\mathbf{p}_t = \mathbf{B}_t\mathbf{E}_t$ where $\mathbf{E}_t$ is the matrix with diagonal elements that are the extent $e_{t,\phi}$ of each feature. The feature density is then given as:

\begin{equation} d_t = \frac{n_t}{-\det(\mathbf{p}_t)}. \end{equation}

The trackability $k_t$ and ambiguous link assignment probability $p$ are then calculated as for the uncorrelated case.